Concetti base di statistica

Prefazione

Nonostante il titolo, questo documento non è, e non vuole essere, una dispensa o un testo didattico di statistica; ma semplicemente una “sintesi per aiutare a ricordare”, per chi già la statistica la conosce, di alcuni elementi fondamentali di statistica descrittiva ed interferenziale, utile per chi si occupa di semplici rilievi analitici e deve rappresentare “significativamente” i propri dati e risultati.

Cifre significative ed arrotondamenti

Il numero di cifre significative indica la precisione della misura ed è il numero minore di cifre necessarie per esprimere una quantità con la precisione richiesta.

Come cifre significative si riportano tutte le cifre certe più la prima incerta.

Nelle operazioni, i risultati non possono avere più cifre significative di quello che ha il dato col maggior numero di cifre significative, nei logaritmi il numero di cifre significative è pari a quello della mantissa.

Negli arrotondamenti non si altera l’ultima cifra che precede quella eliminata se questa è minore di 5; mentre la si aumenta di 1 se questa è maggiore o uguale a 5.

Tipi di errore

Possono essere sistematici, come quelli che rappresentano la prossimità al valore vero (accuratezza); oppure casuali, come quelli che rappresentano la dispersione dei dati attorno al valore medio (precisione).

Rappresentazione dei dati: Distribuzione di frequenza dei dati

In una serie di dati si tabula l’evenienza del dato (modalità) con il numero di volte in cui la modalità compare nella serie (effettivo) e con la frequenza di comparizione (rapporto tra effettivo della modalità e effettivo della serie). Per effettivo e frequenza si possono fare i cumuli.

Se si fa un grafico con in ordinata la frequenza cumulativa ed in ascissa la modalità, si ottiene la curva delle frequenze cumulate.

In caso di variazioni continue, il dato viene suddiviso in classi (intervalli) di modalità. Ogni classe è delimitata da limiti che ne definiscono l’intervallo, la cui differenza rappresenta l’ampiezza e la media dei limiti è il centro. L’ampiezza deve essere scelta in maniera tale che la rappresentazione sia sufficientemente dettagliata, l’ampiezza deve essere uguale a tutti gli intervalli delle classi. Solitamente le classi sono tra 5 e 25 e spesso sono la radice quadrata del numero di dati.

Una delle più frequenti distribuzioni dei dati è quella normale o di Gauss, frutto di azioni concomitanti di più variabili indipendenti fra loro che sommano i loro effetti senza che nessuno di essi abbia a prevalere. La funzione di distribuzione normale è la seguente:

I valori caratteristici della distribuzione normale dei dati sono la media (µ), ovvero il valore centrale della curva di distribuzione, e la deviazione standard (), che rappresenta la dispersione dei dati nella curva di distribuzione. I valori notevoli della dispersione dei dati nella curva di distribuzione normale sono l’intervallo tra che rappresenta il 68% della distribuzione, e l’intervallo tra che rappresenta il 95% della distribuzione.

Una forma utile della distribuzione normale è quella ridotta, la quale presenta la media uguale a zero e la deviazione standard uguale ad uno. In questa distribuzione ridotta, alla variabile “x” vi si sostituiscono i relativi scarti alla media.

La funzione di distribuzione ridotta permette di determinare la probabilità di ottenere un valore abbinabile alla variabile aleatoria “x” entro due limiti, oppure superiore o inferiore agli stessi. La probabilità cumulata per definizione è pari a 1.

Rappresentazione dei dati: Valori caratteristici

I valori caratteristici di una serie di dati, riconducibili a una forma a campana, sono rappresentati da indicatori di posizione che permettono di determinare la forma della serie di dati, la sua localizzazione e la dispersione dei dati.

media aritmetica, mediana e percentili

La media aritmetica è la somma dei valori diviso l’effettivo della serie, ed è uno dei più usati valori caratteristici di tendenza centrale della distribuzione dei dati.

La mediana è quel valore della variabile statistica tal per cui la metà dei valori osservati presenta un valore inferiore e l’altra metà presenta un valore superiore. Anche questo è un valore caratteristico di tendenza centrale, ed al contrario della media aritmetica è poco sensibile ai valori estremi delle serie di dati.

Si calcola ordinando in maniera crescente la serie di dati, quindi, se il numero di osservazioni è dispari, la mediana è il valore centrale della serie (quello che la divide in due gruppi uguali), mentre se il valore è pari, la mediana è il valore medio dei due valori centrali della serie.

I percentili o quantili, sono parametri di posizione che dividono una serie di dati in gruppi non uguali, ad esempio un quantile 0.98 (o 98° percentile), è quel valore che divide la serie di dati in due parti, nella quale una delle due ha il 98% dei valori inferiore al dato quantile. La madiana rappresenta quindi il 50° percentile. I percentili si calcolano come la mediana, ordinando i dati in senso crescente e interpolando il valore relativo al quantile ricercato.

Varianza e deviazione standard

La varianza normalizza la misura della dispersione dei dati attorno al valore medio, e si calcola come media della sommatoria degli scarti quadrati dei singoli valori con la media.

Poiché , allora scomponendo la somma dei quadrati in due termini si ottiene che:

La deviazione standard è la radice quadrata della varianza.

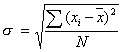
La deviazione standard resa relativa alla media (e riportata in percentuale) da il coefficiente di variabilità, che rappresenta un valore relativo della dispersione dei dati attorno al valore centrale.

Distribuzione della media e valore medio

Se si prendono tutti i possibili campioni, ognuno di dimensione “n”, da qualsiasi popolazione con media µ e deviazione standard di σ, la distribuzione delle medie dei campioni avrà media µ_x = µ e la varianza σ²_x = σ^{2 .} n^-1, e sarà distribuita normalmente se lo sarà la distribuzione di origine, oppure tenderà ad essere normale per un grande numero di campioni.

Il rapporto tra le varianze della popolazione originaria con quella campionaria ci da la dimensione dei campioni estratti dall’origine, quindi la varianza del campione è pari alla varianza della popolazione diviso il numero degli elementi campionati: s² = σ²/n, ovvero s = σ^.n^-0.5. Questo valore rappresenta la deviazione standard delle medie o errore standard della media, e rappresenta l’indice di distribuzione della media campionaria.

Il valore medio “m” della media calcolata sul campione, rappresenta una stima del valore vero della media della popolazione µ, quindi occorre definire un’intervallo all’interno del quale giaccia il valore vero. L’intervallo è definito come intervallo di confidenza e i suoi limiti sono i limiti di confidenza.

Distribuzione di Student

Più la popolazione si riduce e più l’incertezza introdotta usando la varianza del campione “s” per stimare σ aumenta, quindi i limiti di confidenza diventano:

dove il valore di “t”, detto “t di Student” dipende dal numero di gradi di libertà e dal livello di confidenza voluto.

Dal punto di vista pratico il “t” viene usato nei test di significatività per misurare l’accuratezza.

Test di significatività

Quando si effettua un test di significatività occorre definire una ipotesi la cui verità è confermata o rigettata (ipotesi nulla “H₀”), alla quale si contrappone la sua negazione, ovvero l’ipotesi alternativa “H₁”.

I principali test di significatività sono:

- il test “t” o test di accuratezza, che si usa nel confronto tra una media sperimentale con un valore noto o nel confronto tra le medie di due campioni;

- il test “F” o test di precisione che confronta le deviazioni standard di due serie di misure.

Test di accuratezza o Student’s t test

Serve per compensare le interferenza dovute al numero limitato di campioni nella stima di un valore reale. I due casi principali sono: confronto tra una media sperimentale con unvalore noto e confronto tra due medie sperimentali.

Confronto tra una media sperimentale ed un valore noto.

Quando si confronta una media sperimentale (m) di un campione (di dimensione “n” e varianza “s²”) con un valore noto, l’ipotesi nulla è che non vi sia differenza tra la media sperimentale e la media della popolazione “µ”.

Quindi, ricordando che e che di conseguenza , risulta che:

se |t| > t_crit. allora l’ipotesi nulla (H₀) è scartata.

Confronto tra due medie sperimentali.

Due campioni indipendenti di dimensioni n₁ ed n₂ , aventi media m₁ ed m₂, e con varianza s₁ ed s₂, possono considerarsi appartenenti alla popolazione di media µ=µ₁=µ₂ se si verifica l’ipotesi nulla che i due metodi diano lo stesso risultato.

Se le due varianze sono omoscedastiche: s² = [(n₁ – 1) s₁² + (n₂ – 1) s₂² ] / (n₁ + n₂ – 2), allora:

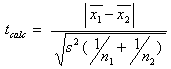
se invece le due varianze sono eteroscedastiche: s² = [(n₁ – 1) s₁² + (n₂ – 1) s₂² ] / (n₁ + n₂ – 2), allora:

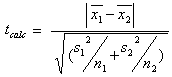
mentre i gradi di libertà sono: .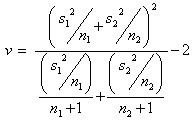

Entrambi i test sono detti a “due code” perché la differenza tra le due medie può esistere in entrambe le direzioni. In alcuni casi però è sufficiente chiedersi se un valore è significativamente maggiore (o minore) di un altro: in questo caso è opportuno un test ad una coda. Nel test ad una coda il t_crit. Per P=0.05, è quel valore che è superato con una probabilità del 5%. Per la simmetria della distribuzione, questa probabilità è la metà di quella che si ottiene in un test a due code, quindi il valore appropriato di “t” lo si trova nella colonna P=0.10.

Tabella dei t_crit. Per diversi gradi di libertà e per probabilità di esclusione dall’intervallo –t:t.

Probabilità di esclusione (2 code)	0.2	0.1	0.05	0.02
Probabilità di esclusione (1 coda)	0.1	0.05	0.025	0.01
Gradi libertà
1	3.078	6.314	12.706	31.821
2	1.886	2.92	4.303	6.956
3	1.638	2.353	3.182	4.541
4	1.533	2.132	2.776	3.747
5	1.476	2.015	2.571	3.365
8	1.397	1.86	2.306	2.896
10	1.372	1.812	2.228	2.764
15	1.341	1.753	2.131	2.602
20	1.325	1.725	2.086	2.528
30	1.310	1.697	2.042	2.457
60	1.296	1.658	2.000	2.390
infinito	1.282	1.645	1.960	2.326

Test di Precisione o Test F

Può essere usato per verificare se un metodo è più preciso di un altro (test ad una coda) o se le due deviazioni standard differiscono significativamente (test a due code).

Il test F considera il rapporto tra le due varianze dei campioni, scritto in maniera che F>1:

L’ipotesi nulla è verificata se le popolazioni da cui sono stati estratti i campioni sono normali e le varianze delle popolazioni sono identiche; se F_calcol.> F_crit. allora l’ipotesi nulla è rigettata.

Il valore di F_crit. è disponibile su apposite tabelle.

Confronto tra più di due medie: ANOVA

Uno dei più diffusi metodi di confronto tra due medie è il già citato test T, ma quando le medie da confrontare sono in numero maggiore di due, solitamente si ricorre all’analisi della varianza (ANOVA).

L’ANOVA consente di confrontare fra loro due o più medie, di valutarne contemporaneamente l’effetto di due o più fattori di variazione sulle stesse medie e di stimarne gli effetti.

L’ipotesi nulla (H₀) è verificata se il fattore controllato NON ha alcuna influenza sui risultati delle prove.

ANOVA ad una via

Permette di determinare due fonti di varianza del dato: quella dovuta agli errori casuali della misurazione e quella dovuta ad un fattore controllato.

L’ANOVA quindi scompone la varianza totale in varianze parziali relative ai vari fattori di variazione.

L’ANOVA è applicabile se la popolazione di origine ha distribuzione normale e se le varianze sono omogenee (omoscedastiche).

Noto che la varianza di un campione (s²) viene calcolata come la somma dei quadrati degli scarti dalla media diviso “n-1”, la sola somma dei quadrati degli scarti è detta devianza (d).

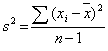
Per il calcolo si tabulano i campioni con le relative repliche e si calcola la media per campione e la media generale:

Campione	Replica 1	Replica 2	Replica 3	Replica i	Replica n	media repliche
1	x11	x12	x13	x1i	x1n	1
2	x21	x22	x23	x2i	x2n	2
j	xj1	xj2	xj3	xji	xjn	j
h	xh1	xh2	xh3	xhi	xhn	h
					media gen.

Se l’ipotesi nulla è vera (non vi è differenza tra le medie) tutti i dati appartengono alla stessa popolazione.

La media del campione J e:

La media generale è:

La devianza totale e:

La devianza totale si può scomporre in SS_R (variazione entro i gruppi o misura della variazione residua o aleatoria) e in SS_A (variazione tra i gruppi o variazione dovute a trattamenti diversi):

Per stimare le varianze occorre calcolare i gradi di libertà:

SS_T (nh-1)

SS_R (h^.(n-1))

SS_A (h-1)

Prima di procedere occorre effettuare un test F:

poi si confronterà F_calcolato con F_tabulato. Se F_calcolato > F_tabulato, allora la differenza tra le medie è significativa, quindi anche il trattamento è significativo.

ANOVA a due vie

In questo caso ogni misura è classificata rispetto a due fattori: trattamento e blocco.

Il confronto, col test F, fra la varianza fra i trattamenti (o fra i blocchi) e la varianza totale, permette di valutarne la significatività degli effetti dei trattamenti (o dei blocchi).

Il numero totale delle misure è N = r c, dove “r” è il numero totale dei blocchi e “c” quello dei trattamenti.

Le fonti di variazioni sono quindi tre: tra i blocchi, tra i trattamenti e l’errore sperimentale.

Fattore A\ fattoreB	trattamento 1	trattamento 2	trattamento 3	trattamento j	trattamento c	Totale blocchi
Blocco 1	x11	x12	x13	x1j	x1c	T1
Blocco 2	x21	x22	x23	x2j	x2c	T2
Blocco i	Xi1	Xi2	Xi3	xji	Xic	Ti
Blocco r	Xr1	Xr2	Xr3	Xrj	Xrc	Tr
Totale trattamenti	T°1	T°2	T°3	T°j	T°c	T

Le formule di calcolo sono le seguenti:

Variazione	somma dei quadrati	gradi libertà
totale		N-1
tra trattamenti		c-1
tra i blocchi		r-1
residua	per sottrazione	per sottrazione

Dove T²/N è un fattore di correzione che serve per semplificare il calcolo.

Data la complessità di calcolo è conveniente utilizzare appositi pacchetti informatici per l’escuzione di questo genere di calcoli.